注：涉及大量概率论中的数学推导，不对其推导过程做详细解释，只说明结果的意义是什么

DDPM是什么？

一种生成模型，其核心思想是通过逐步将噪声添加到数据中，学习如何去噪以恢复原始数据。

先讲一下生成式模型

目标

生成出与现实中的数据/我们给出的训练集类似的数据

通用思想

真实的数据（图像、音频等）的分布可能十分复杂，并不方便我们用一个数学模型去描述，也就不能做出好的生成任务。

与此同时，一些简单的分布（高斯、二项）在数学上已经有很完备的理论和工具去描述、处理。于是生成式模型的核心思想就变为，找到把现实数据处理成简单分布，并且能够从简单的分布还原出数据的一套方法。

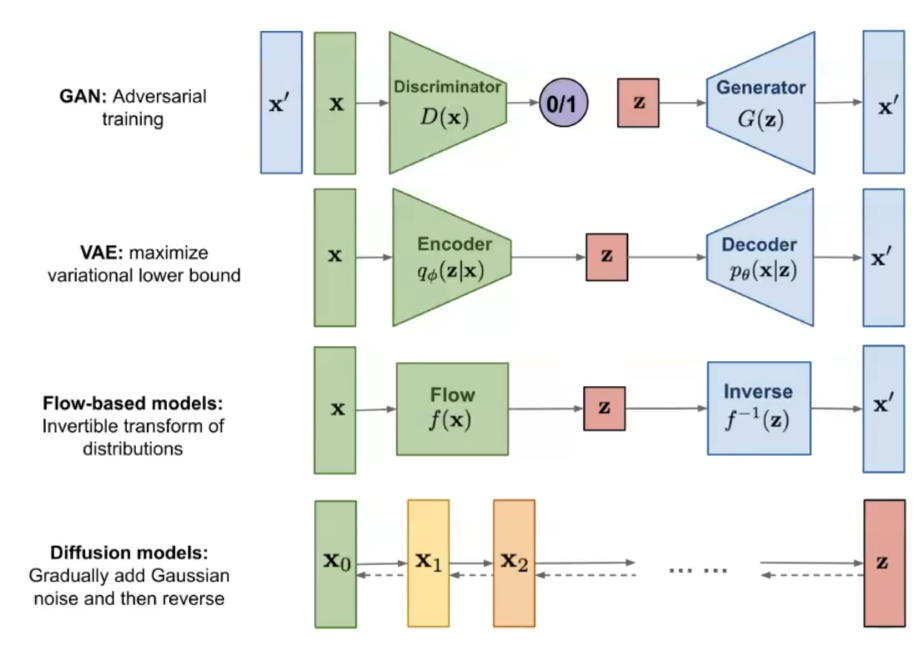
例如，VAE和Flow模型的latent space中就是标准高斯分布。而在Diffusion Models也是如此，我们通过不断添加微小的高斯噪声，使原始分布逐渐趋近于标准高斯分布。（为什么一直加噪声就趋向N(0,1)的原因后面说）

优化目标（设计Loss的源头）

训练目标是使得生成出的数据X的分布与真实数据的分布越接近越好。

θ：网络的参数
PθP_\theta：网络生成出的分布
PdataP_{data}：真实数据的分布

如何衡量“接近”？→ 极大似然估计（找到生成出数据集{x1,x2,⋯ ,xm}\{x_1,x_2,\cdots,x_m\}中各个元素概率之和最高的网络参数θ）

极大似然估计 → 生成出来的数据的分布 与 原始数据的分布 的 KL散度

θ∗=argmax∏i=1mPθ(xi)\theta^*=argmax\prod_{i=1}^mP_\theta(x^i)

而生成式模型中，我们一般无法直接把优化目标设为“最大化生成出x的概率P(x)”

只能如右图所示，最大化logP(x)logP(x)的下界

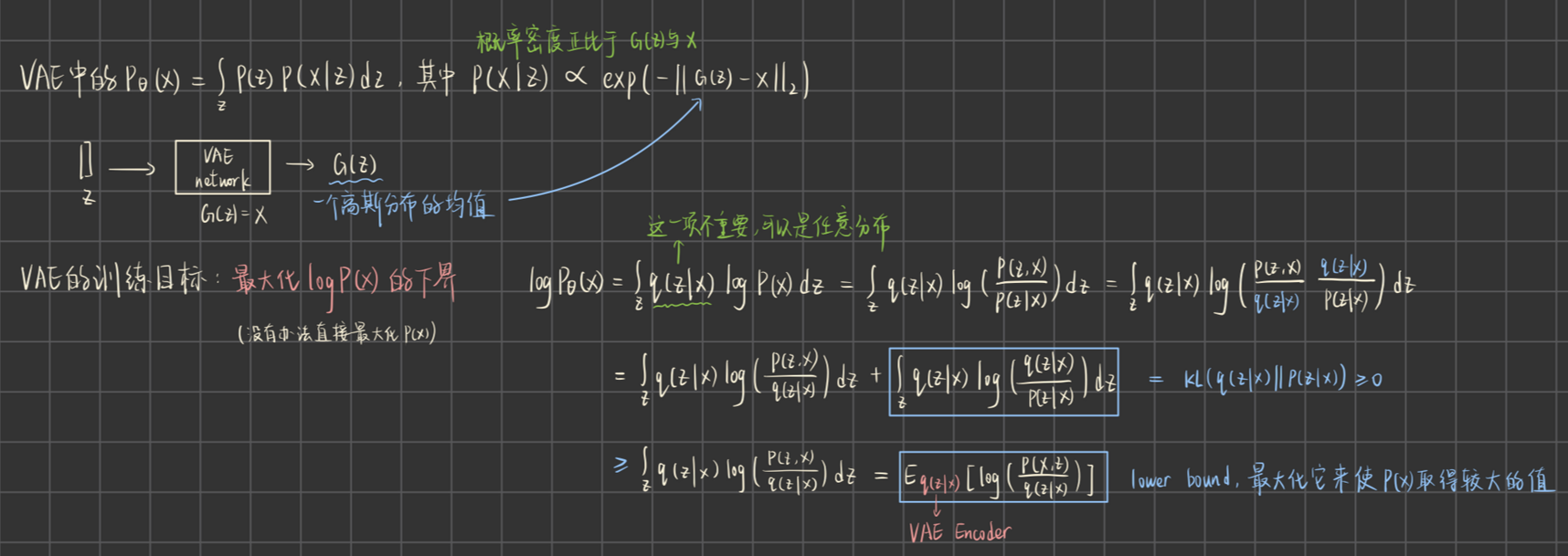
现在，正式开始讲DDPM

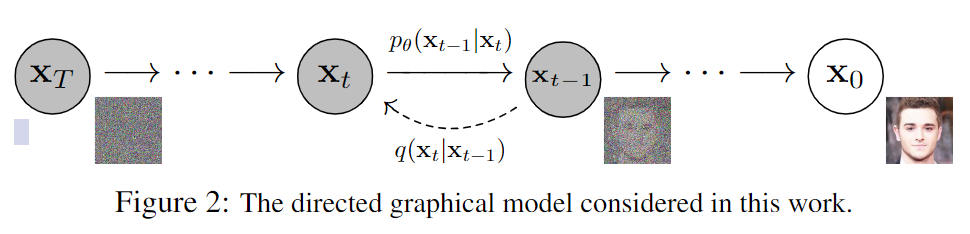
DDPM的整体结构是一个马尔科夫链。

前向过程：对原始图像X0X_0不断添加微小的高斯噪声，最终变为一个标准高斯分布的噪声XTX_T

后向过程：对随机采样出来的噪声XTX_T，用神经网络θ\theta去拟合每一步加噪的反过程，从XtX_t预测Xt−1X_{t-1}的分布，用pθ(xt−1∣xt)p_\theta(x_{t-1}|x_t)的过程一步步生成对应的X0X_0

Untitled

如何训练：

  1. 原始图片X0X_0、随机数tt、加噪得到XtX_t
  2. 对于反向过程中的神经网络，输入XtX_t和tt，预测当前加到图片上的噪声
  3. 预测出的噪声和实际加的噪声做L2 Loss，反向传播
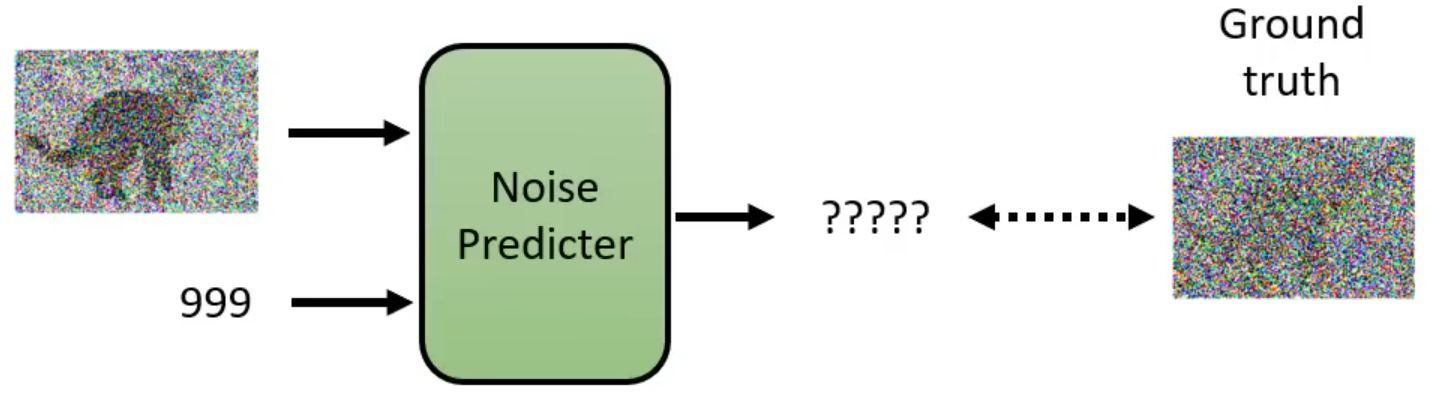
Untitled Untitled

如何生成：

  1. 从N(0,1)随机采样出噪声XTX_T
  2. 循环做T次“预测噪声 + 去噪”
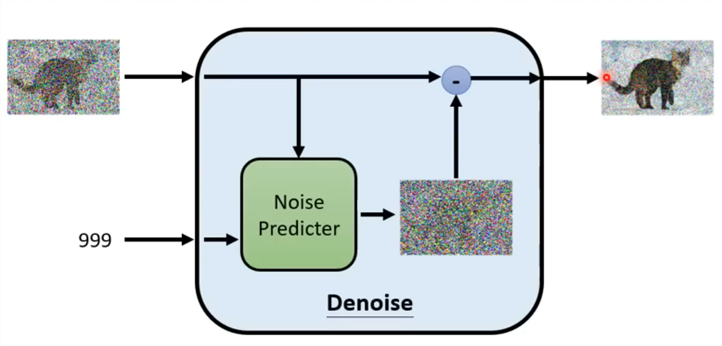
Untitled

下面依次解答三个问题：

  1. 为什么一直加噪XTX_T就服从标准高斯
  2. 为什么反向过程是在预测噪声
  3. 如何设计损失函数，使得网络能够预测噪声

1、为什么一直加噪XTX_T就服从标准高斯

前向过程的公式：Xt=1−βt⋅Xt−1+βt⋅ϵX_t = \sqrt{1-\beta_t}\cdot X_{t-1} + \sqrt\beta_t \cdot \epsilon

其中β们是一个非常小的线性增大的列表，用代码写出来就是右边的样子（n_steps=T）

1
self.beta = torch.linspace(0.0001, 0.02, n_steps).to(device)

按照右边的推导过程，我们可以直接用X0、ϵ、αt(=1−βt)X_0、\epsilon、\alpha_t(=1-\beta_t)表示出来

按照重参数采样技巧得Xt∼N(αˉt,1−αˉt)X_t \sim N(\sqrt{\bar\alpha_t}, 1-\bar\alpha_t)

当T非常大的时候，αtˉ=α1⋅α2⋯αt\bar{\alpha_t}=\alpha_1 \cdot \alpha_2 \cdots \alpha_t 由一堆（0，1）区间内的α乘起来，趋近于0，

而1−αˉt1-\bar\alpha_t趋近于1，所以XT∼N(0,1)X_T\sim N(0,1)

Untitled

前向过程的单步转移概率推导如右边，结果如下

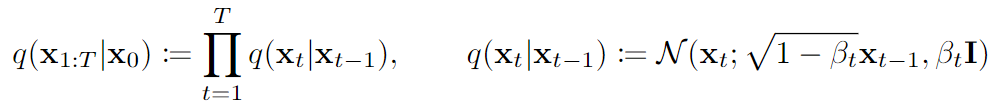
Untitled

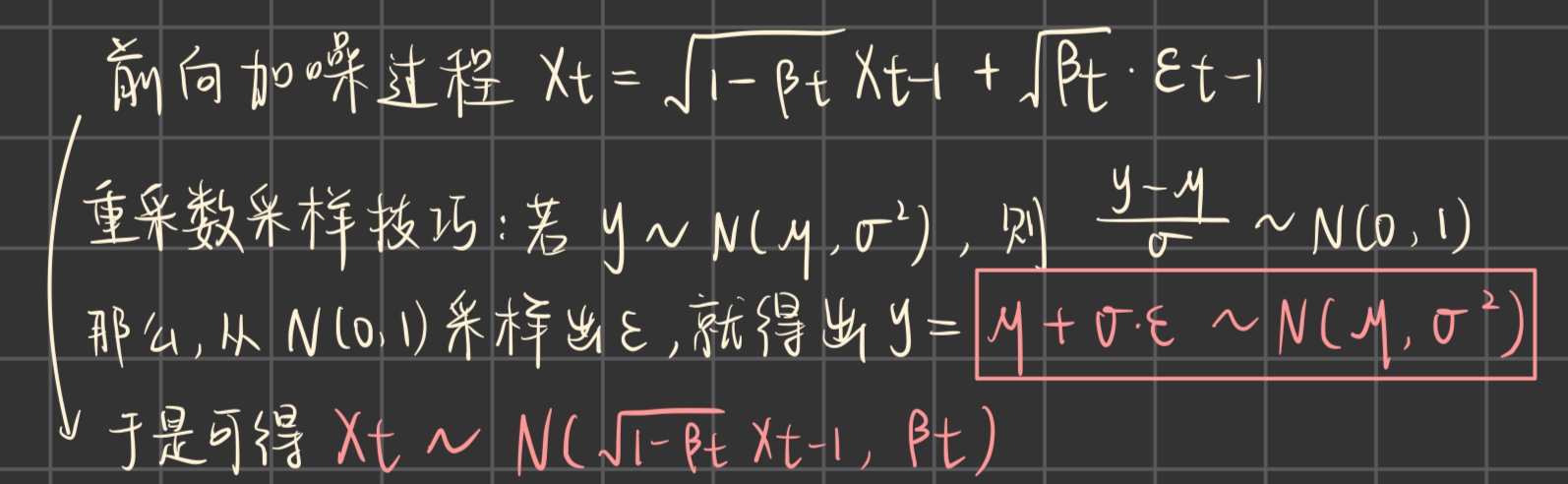
2、为什么反向过程是在预测噪声

注：以下讨论的是理论上的反向过程应该是怎样，所以用q表示

在训练过程中，已知X0X_0的情况下，我们其实是可以直接推导出单步去噪（XtX_t→Xt−1X_{t-1}）的表达式的。并且会发现，q(Xt−1∣Xt)q(X_{t-1}|X_t)这个过程，依然是一个高斯分布。推导如右。

那么，反向过程就应该是去模拟这个高斯分布的转移过程。我们预期的生成图像过程是直接随机采样一个XTX_T就开始的，是not given X0的。右边这个在given X0的情况下得出的式子中，没有显式的X0出现，那一定是有我们在反向过程中不知道的参数。

观察后发现是前向过程中加入的噪声ϵt\epsilon_t

所以denoiser中网络的工作是在预测噪声

3、如何设计损失函数

真正生成图像的时候，我们用网络Pθ(Xt−1∣Xt)P_\theta(X_{t-1}|X_t)来模拟q(Xt−1∣Xt)q(X_{t-1}|X_t)

因为后者是一个高斯分布过程，输入XtX_t和tt，输出预测的ϵt\epsilon_t

所以Pθ(Xt−1∣Xt)P_\theta(X_{t-1}|X_t)设计为如下表达式：

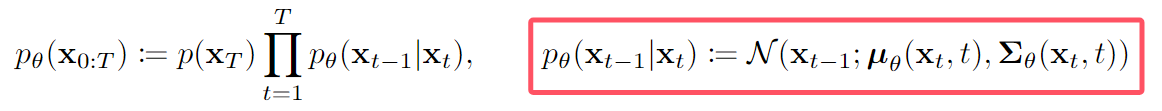
Untitled

基于最前面写的“生成式模型的优化目标”，作者给出了需要最小化的负对数下界（最大化正下界，所以最小化负下界），其推导在论文的附录，如右所示。

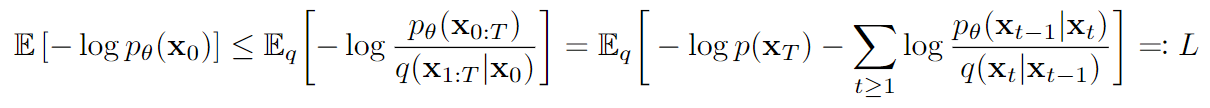
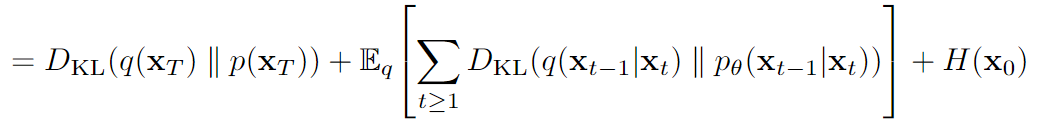
Untitled Untitled

继续推导，得出如下需要最小化的式子

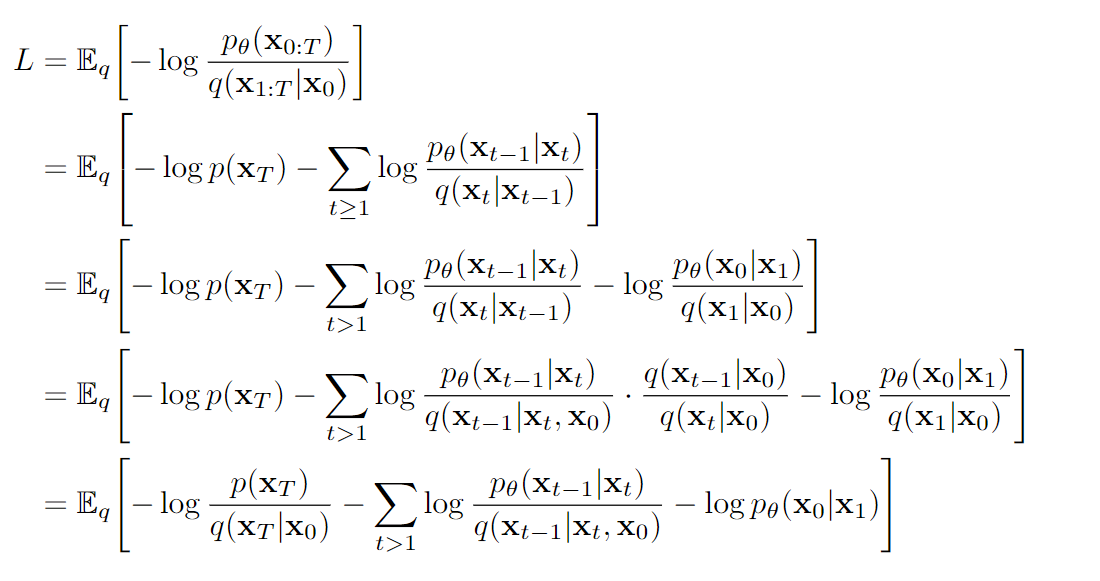
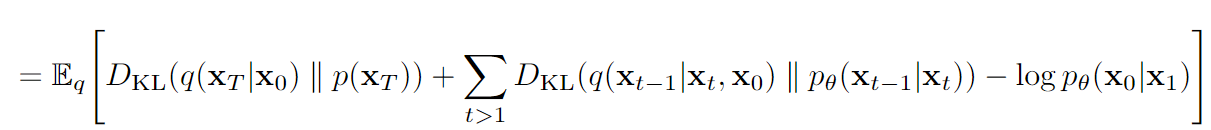
Untitled Untitled
  • 第一项：前向过程中最后得到的噪声，要和真正从N(0,1)采样的噪声，KL散度小，这与网络无关！
  • 第三项：可以理解成最大化x0和x1的相似度，这也是超参数β决定的，与网络无关！

于是只需要最小化第二项这个KL散度

我们把这两个概率服从的正态分布写出来：

Untitled

要让两个正态分布接近，就是均值接近+方差接近。而在实践中，作者固定了方差（各种diffusion的文章表明，优化方差几乎没什么收益，不如单干均值）

把两个均值相减，常数项和已知项不看，发现就是ϵt−ϵθ\epsilon_t-\epsilon_\theta，因此将损失函数设计为预测出噪声和实际噪声的L2 Loss

过算法

训练算法（Unet训练的过程）

Untitled 
1
2
3
4
5
6
7
8
9
1. 循环：
	2. 每次从数据中抽取一个样本
	3. 从1到T中随机选择一个时间t
	4. 在高斯分布上面采样随机噪声
		5.1 把X0和随机噪声按照公式相加，产生Xt
						这个公式直接从0-t，而不用循环加噪，论文中有推导
		5.2 Unet通过t、Xt来预测噪声
		5.3 将预测出来的噪声和实际噪声，计算L2 loss（均方误差），然后计算梯度更新权重
	6. 循环直到收敛

采样算法（生成图像的过程）

Untitled 
1
2
3
4
5
1. 在标准正态分布中，采样出一个噪声XT
2. 循环T(通常是1000)次的去噪过程
	3. 从标准正态分布中采样一个z
	4. 按照Pθ的公式去噪得到X{t-1}，其中theta直接从beta得来，然后加上一个噪声
5. 循环完T次就得到生成出的图像X0，返回

这里最后还要加的这个σtz\sigma_t z很反常，前面也没有提及

实际上，这是为了在生成式模型中让每次的output不固定

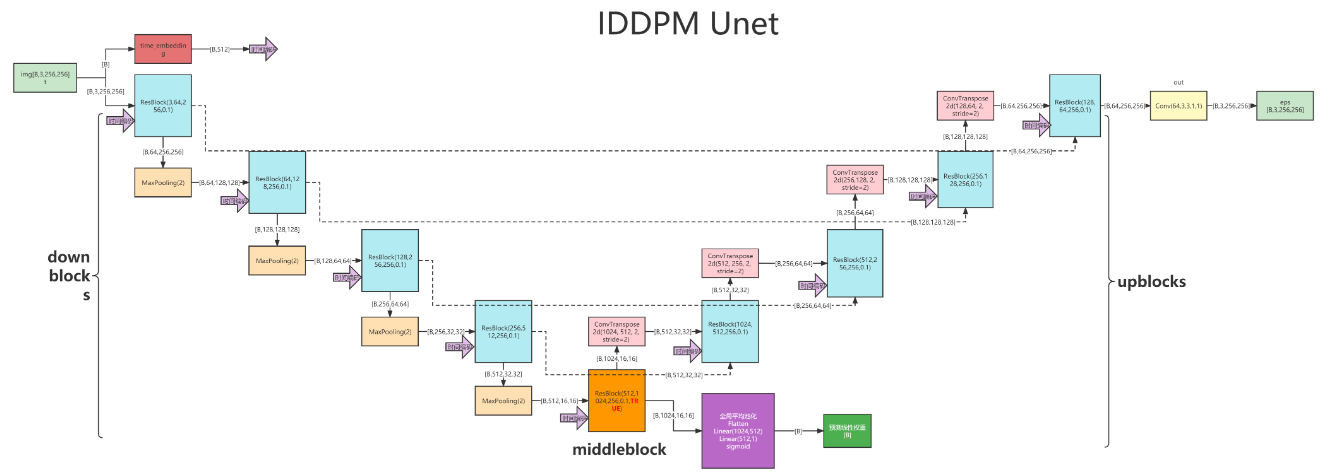
Denoiser中使用的网络：UNet

原始的Unet是一个用于医学图像分割任务的网络，通过卷积下采样，然后直接逆卷积上采样，来对图像的大体区域进行划分

在DDPM中使用的Unet进行了如下改变：

  1. 使用Embedding，将时间t融入了预测中
  2. 把卷积层都换成了resnet
  3. 加入了Attention模块，增强特征表达能力和捕捉全局依赖关系，使得生成的图像更加逼真。
Untitled